『孤独素数』的定义与搜索算法

发表于 分类于

问题

在知乎上看见了个有意思的问题：

孤独素数：
一个素数 P 通常可以分为两个殆素数之和，其序数与对应的殆素数的素因子序数同时满足：
\begin{equation*}
\begin{cases}
P = \prod p_i + \prod q_i \\
\pi(P)=\prod \pi(p_i) + \prod \pi(q_i)
\end{cases}
\end{equation*}
例如 $11 = 2*3 + 5$，同时有 $\pi(11) = 5 = \pi(2)\pi(3) + \pi(5) = 1\cdot2 + 3。$
但也存在一些素数，任意分法均不能满足上述规则，称为孤独素数。

看见这题我是懵逼的，懵逼树上懵逼果，第一步直接撞死在黎曼猜想了，想不到在 $\pi(p)$ 还没有明确公式解的情况下怎么去判断孤独素数的规律。但至少这个看起来是个简单而有趣的编程练习题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
// 欧拉筛法获得 n 以内的素数表
function EulerSieve(n) {
    const primes = [];
    let eularboard = new Array(n + 1).fill(true);
    for (let i = 2; i <= n; i++) {
        if (eularboard[i]) {
            primes.push(i);
        }
        for (let j = 0; j < primes.length; j++) {
            if (i * primes[j] > n) break;
            eularboard[i * primes[j]] = false;
            if (i % primes[j] === 0) break;
        }
    }
    return primes;
}
const primes = EulerSieve(10 ** 6);

// 计算殆素数的素因子序数乘积，并使用使用 dp 避免重复的因式分解
const dp = [];
function factorOrdersProduct(n) {
    if (n === 1) return 0;
    if (dp[n]) return dp[n];

    const init = n;
    const sqrt_n = Math.floor(Math.sqrt(n));
    let indices = 1;
    for (let i = 0; i < primes.length; i++) {
        const p = primes[i];
        if (p > sqrt_n) break;
        while (n % p === 0) {
            indices = indices * (i + 1);
            n = n / p;
            if (dp[n]) {
                indices = indices * dp[n];
                n = 1;
                break;
            }
        }
        if (n === 1) break;
    }

    if (n > 1) {
        const idx = primes.indexOf(n);
        if (idx === -1) throw new Error(`Math crisis ${n}`);
        indices = indices * (idx + 1);
    }

    dp[init] = indices;
    return indices;
}

// 寻找孤立素数，将每个素数分解成两个殆素数，然后计算殆素数的素因子序数乘积
const lonelyPrimes = [];
for (let i = 0; i < primes.length; i++) {
    const p = primes[i];
    let lonely = true;
    for (let m = 2; m < p / 2; m++) {
        if (factorOrdersProduct(m) + factorOrdersProduct(p - m) === i + 1) {
            lonely = false;
            break;
        }
    }
    if (lonely) {
        lonelyPrimes.push(p);
    }
}

console.log(lonelyPrimes);
// 2, 3, 211, 277, 541, 631, 653, 1259, 2797, 2897, 4391, 5279, 5323, 5381, 5527,  6113, 6547, 7177, 7523, 7993, 8147, 8513, 9157, 9661, 10211, ...

实测下来 Apple M1 上计算 $10^6$ 以内孤独素数约 3.5 秒，$10^7$ 以内约 180 秒。

优化

整体来看上述代码是清晰的，先用欧拉筛获得素数数组，再根据孤独素数的定义逐个验证。由于殆素数分解是必然有解的，实际上就是验证第二条件序列数的运算是否成立。通过 dp 暂存已经计算过的结果，可以大大提高效率。但直观来看，还有一些可以优化的小点：

  1. 在规模不大的时候，可以使用字典对象储存素数与其序数的键值对，替代 primes.indexOf(n)。一个对象可以容纳 2^24 个键值对，即最大素数为 $p_{(2^{24})}$，查询得知 $p_{16777216}=310248241$，足够大了。更大规模也可以使用若干个字典对象来应对。
  2. 如果一个殆素数因子序数乘积已经超过了当前素数序数，可以提前结束。但需要考虑每次增加的判断带来的损耗是否小于节约的时间。考虑到：$\pi(p) \approx p / \ln p$，殆素数 m 大概率为合数， $\pi(m) <\prod_i(m_i/ln m_i), m = \sum_i m_i$，m-q 同理。而 $lnp$ 显然是大于 1 的，因此可以认为这种提前结束的情况几乎不存在。在极端情况下，m=2，p 与 p-2 为孪生素数，也只是等于序列数的和。因此这一条更大可能是负面的。
  3. 使用 UInt32Array 等定长数组优化，这个我不是很喜欢。我知道它有效，但总觉得将语言特性也视为算法本身的优化的话，汇编就是唯一可用的语言了。

以及一个可能存在的大优化点：

在欧拉筛获得素数的过程中，我们已经把所有的合数都计算过一遍了

这意味着 factorOrdersProduct(n) 函数的计算过程，与筛法取素数的计算过程本身是有大量重合的。在题目的定义下，素数 p 的两个加数几乎就覆盖了从 1-n 的所有合数，也就是筛法求素数中被筛去的数，以及筛选这个动作本身也是有价值的。

值得一提的是，在因数分解相关算法中有个 SPF(Smallest Prime Factor) 算法。它与欧拉筛是完美配合的。简单地说，SPF 分为两步：

  1. 在筛法取素数过程中，保留合数而不是直接筛去，并记录每个数最小质因数。
  2. 在因数分解过程中，使用类似递归的方法，根据最小质因数快速计算各合数的全部因子。

在第 1. 步中将 SPF 与欧拉筛结合，并将第 2 步中的计算因子数组改为计算因子序数乘积，即可得到更高效的搜搜代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
const n = 10 ** 6;
const spf = new Uint32Array(n + 1).fill(0);
const primes = [];
const primeIndex = new Map();
const product = new Uint32Array(n + 1);

// 构建SPF和素数序号
for (let i = 2; i <= n; i++) {
    if (spf[i] === 0) {
        spf[i] = i;
        primes.push(i);
        primeIndex.set(i, primes.length); // 记录素数序号
    }

    for (let j = 0; j < primes.length; j++) {
        const p = primes[j];
        const ip = i * p;
        if (p > spf[i] || ip > n) break;
        spf[ip] = p;
        if (i % p === 0) break;
    }
}

// 直接计算因子序数乘积
product[1] = 1;
for (let i = 2; i <= n; i++) {
    const p = spf[i]; // 最小质因数
    const prev = i / p;
    product[i] = product[prev] * primeIndex.get(p);
}

// 寻找孤立素数
const lonelyPrimes = [];
for (let idx = 0; idx < primes.length; idx++) {
    const p = primes[idx];
    const target = idx + 1; // primeIndex[p]
    const half = Math.floor(p / 2);
    let lonely = true;
    for (let m = 2; m < half; m++) {
        if (product[m] + product[p - m] === target) {
            lonely = false;
            break;
        }
    }
    if (lonely) lonelyPrimes.push(p);
}

优化结果是 $10^6$ 以内约 0.8 秒，$10^7$ 以内约 52 秒，$10^8$ 约 8900 秒。

在 JS 实现中，对于相同的查询请求，性能排序大约是 Uint32Array > Array $\approx$ Object > Map。但 V8 引擎存在 bug，导致 Array 或 Object 在用作 primeIndex 时出现了预料之外的错误，不得不用 Map()。这就是为什么我不喜欢基于语言特有数据结构的优化。而相同的 python 代码虽然可以天然地支持更大的数字而无需考虑这些异常，也无需考虑默认 2GB 的内存上限，但代价是慢得多的计算速度以及单位计算量下更大的内存占用。在计算规模上升后还不如 nodejs 实用。

观察

在有了高效的孤独素数搜索算法以后，可以对其序列进行一些观察。

  1. 分布。

从计算结果看，孤独素数很稀疏，且存在较大的波动。但计算到 1 亿，以 10 万为一段统计其出现的频率，发现和素数本身的分布趋势是大致一致的。

分布

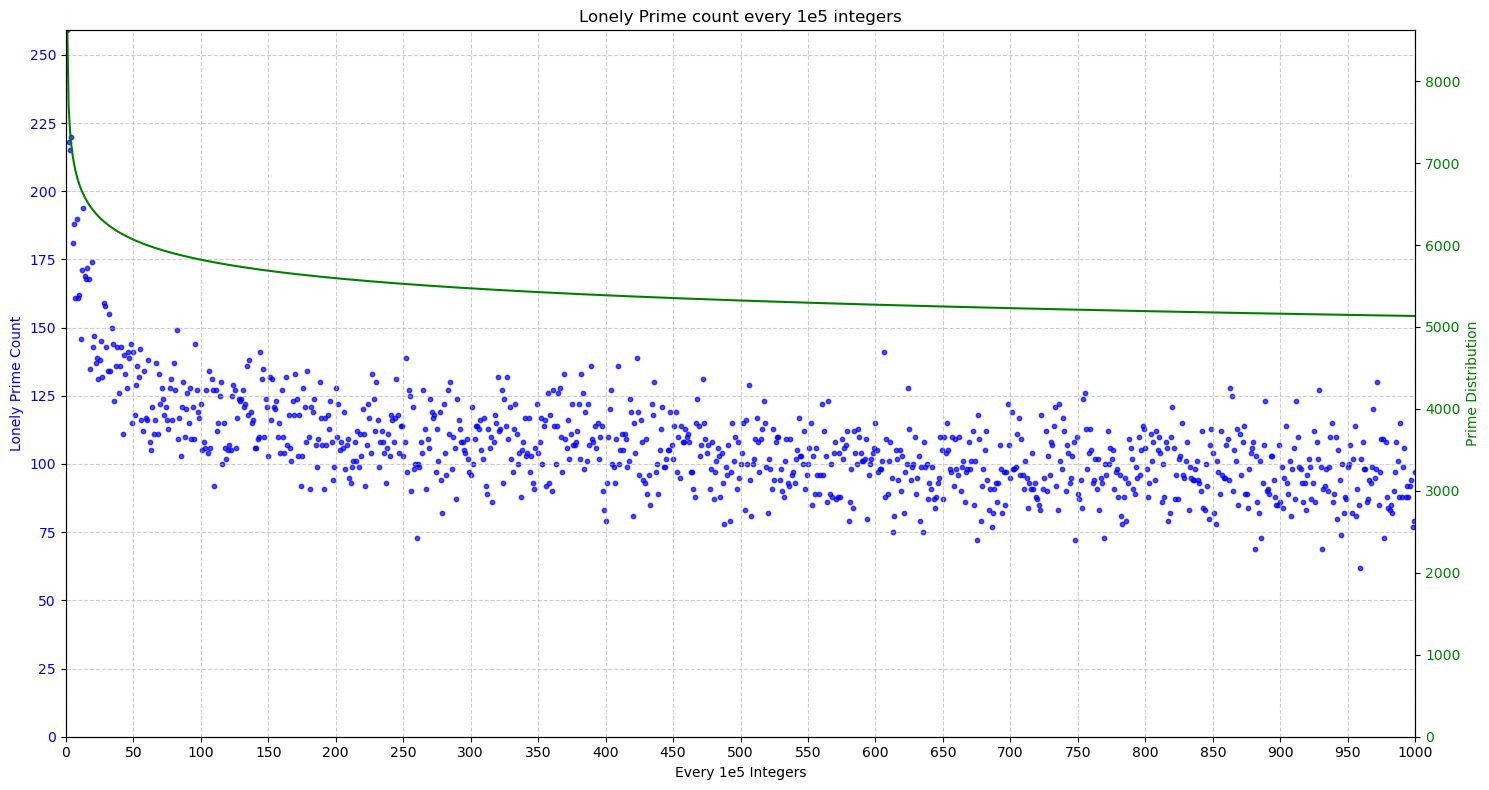
绿色为素数数量分布参考线 $\pi(p)=p / \ln p$

  1. 解的分布。

对于非孤独素数，第一个解往往在 m 较小时就出现了。一般地，对于 p = m + q 的情况，上述算法是从 m = 2 开始逐项验证的，等效于从 p 左边的所有数中取任意两个，使 $\pi(p)$ 有解。先来看一下所有数的因子序数积的分布情况。

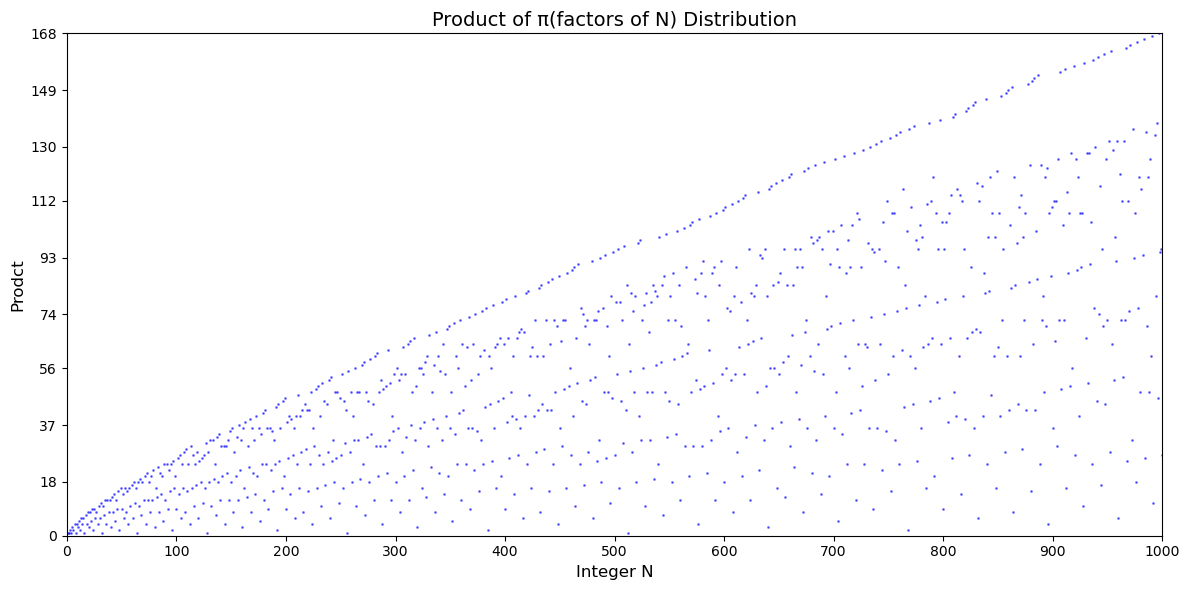
前1000个整数的因子序数积的分布

前 1000 个整数的因子序数积的分布

前30000个整数的因子序数积的分布

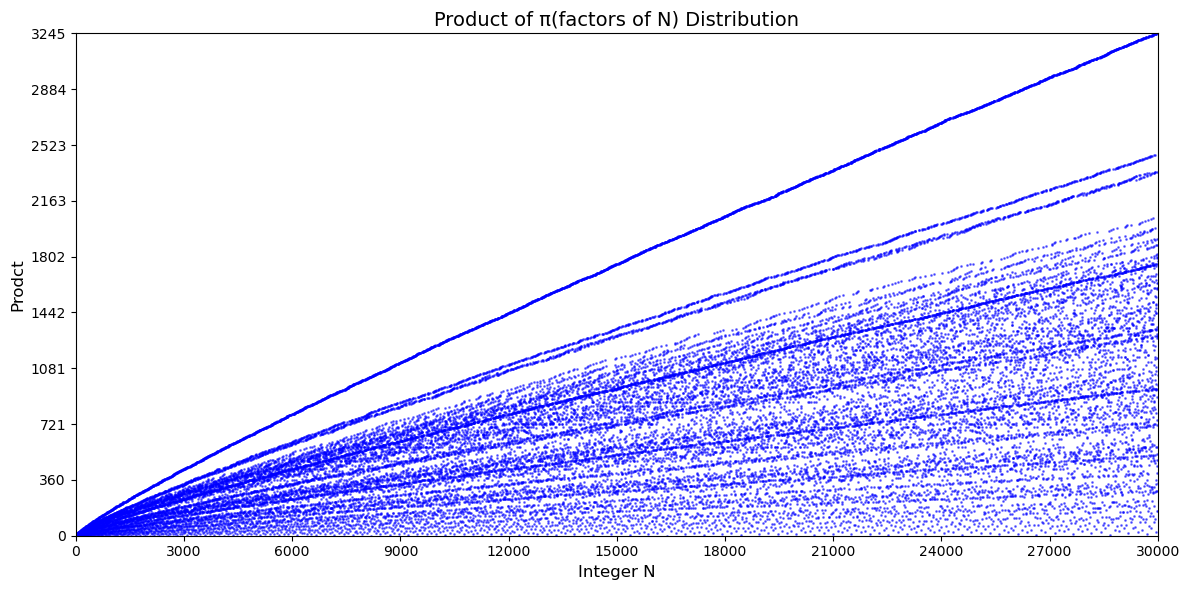
前 30000 个整数的因子序数积的分布

从图中我们发现，整数的因子序数积的分布出现了明显的原点出发放射状图样，最上面一条显然是质数和其对应的序列数。随着 x 轴放大点数密集，放射线变得更为清晰。因此我们进行局部放大并标注具体数据后如下：

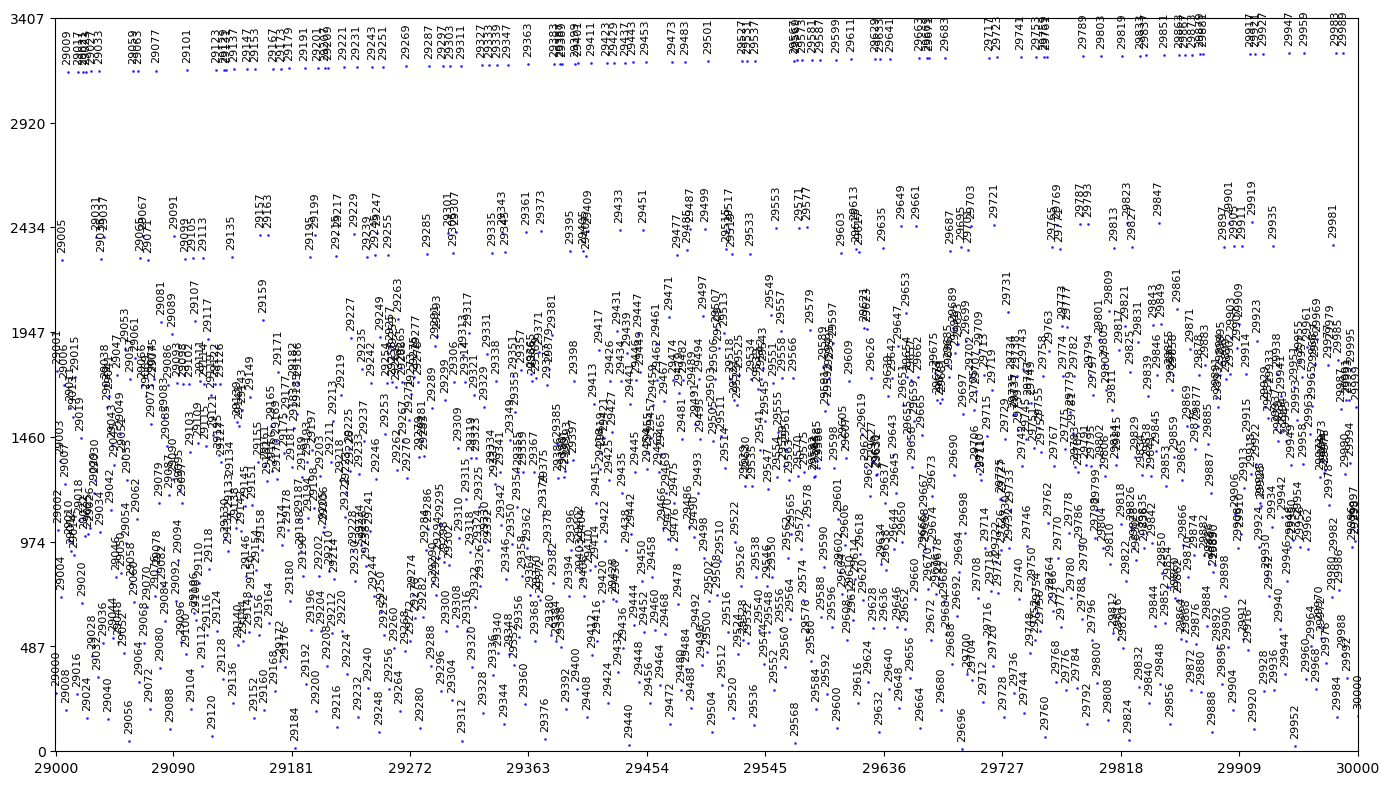
29000到30000整数的因子序数积的分布

29000 到 30000 个整数的因子序数积的分布及数值标注

经过简单计算，就可以发现素数线以下的第二条线是 $3\times素数$，再下面第三条线是 $5\times素数$。

根据图像发现一个推论，若素数 p' 与 p $\frac{p'}{p} \approx \frac{1}{3}$，则 $\frac{1}{3} < \frac{\pi(p')}{\pi(p)} < \frac{1}{2}$，所以才有 $3\times素数$ 线稳定在素数线下。

当 p 足够大时，$\pi(p)\approx p / ln(p)$，假设存在一个与 p 几乎相等的殆素数 3p'。则有：
$$ \frac{\pi(3)\cdot\pi(p')}{\pi(p)}\approx \frac{2p}{3ln(p/3)} / \frac{p}{lnp} = \frac{2}{3}\cdot\frac{lnp}{lnp-ln3}$$
令 $t=lnp$, $c=ln3$，则比值 $r(t)=\frac{2}{3}\cdot\frac{t}{t-c}$，其中$t>c$ ，即$p>3$。

  • 若 $r(t)>1$，则 $2t>3t-3c \Rightarrow t<3c \Rightarrow lnp<ln27 \Rightarrow p<27$
  • 若 $r(t)=1$，则 $p = 27$
  • 若 $r(t)<1$，则 $p > 27$

也就是说 在 p 足够大时，$\pi(p) > \pi(3)\cdot\pi(p')$，因此殆素数 3p' 构成的因子序数积的线一定在 $\pi(p)$ 下方。

以同相方法，容易比较 2p'、5p' 等不同殆素数构成的线条的相对位置。进一步地，n 阶殆素数也可以以类似的方法确定相对顺序。

特殊地，因为$\pi(2)=1$，所以 $2^n$ 是最底部恒等于 1 的横线。

  1. p = m + q

根据上一条的结论，对于一个殆素数，每增加一个因子，它的因子序数积都是变小的，因为对任意 p 都有 $\pi(p)<p$。所以通常来说，其中一个值是较小的质数，会让等式成立的概率更大。

如果两个都是殆素数，最优情况也至少是 $p=3p_1+5p_2$，如果 p 足够大，此时要求 $p/lnp = 2p_1/lnp_1+4p_2/lnp_2$，若 m 与 n 大小类似，容易导致 $p_1, p_2$ 过小。

也就是说，$\pi(p)=\prod \pi(p_i) + \prod \pi(p_j)$ 等式要成立，可以调节的空间大小就是 $p/lnp - (p_i/lnp_i + p_j/lnp_j)$，这个当然没有稳定解，但从趋势上容易理解，m q 差异越大的，殆素数因子越少的，越容易得到解。

  1. 特例与猜想
  • 孪生素数中较大的一个，一定不是孤独素数，这结论还挺文学的。
  • 有无穷多个孤独素数。
  • 指定 m 为任何 2 以上整数，都可以找到 p 与 q 使得公式成立。

得不出什么普遍性的结论，思而不学民科一下。